Using C Program Find Kruskal’s Algorithm For Minimum Spanning Tree

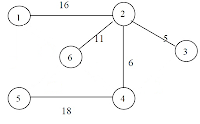
Before

After

#include< stdio.h>
#include< conio.h>
#define INFINITY 999
typedef struct Graph
{
 int v1,v2,length;
}GR;
GR G[20];

int tot_edge,tot_node;
void create();
void krushkal();
int find(int,int[]);
void merge(int i,int j,int parent[]);

void main()
{
 clrscr();
 printf("\n----------------------------------------------------");
 printf("\nKRUSHKAL`s MINIMUM SPANNING TREE ALGORITHM");
 printf("\n----------------------------------------------------");

 create();
 printf("\n Enter any key to see Minimum Spanning Tree?");
 getch();
 krushkal();
 getch();
}






void create()
{
 int k;

 printf("\n Enter Number of nodes in the Graph:");
 scanf("%d",&tot_node);

 printf("\n Enter Number of Edges in the Graph:");
 scanf("%d",&tot_edge);
 printf("\n--------Enter edges and length----------\n");
 for(k=0;k< tot_edge;k++)
 {
  printf("\nEnter edge in form {v1,v2}:");
  scanf("%d %d",&G[k].v1,&G[k].v2);

  printf("\nEnter Length from %d to %d:",G[k].v1,G[k].v2);
  scanf("%d",&G[k].length);
 }
}
void krushkal()
{
 int count,k,i,j,v1,v2,tree[20][20],pos,parent[20];
 int sum;
 int find(int v2,int parent[]);
 
 count=0;
 k=0;
 sum=0;

 for(i=0;i< tot_node;i++)
  parent[i]=i;
 while(count!=tot_node-1)
 {
  pos=Minimum(tot_edge);
  if(pos==-1)
   break;
  v1=G[pos].v1;
  v2=G[pos].v2;
  i=find(v1,parent);
j=find(v2,parent);


if(i!=j)
  {
   tree[k][0]=v1;
   tree[k][1]=v2;
   k++;
   count++;
   sum+=G[pos].length;
   merge(i,j,parent);
  }
  G[pos].length=INFINITY;
 }

 if(count==tot_node-1)
 {
  printf("\n----------------------------------------------------");
  printf("\n The minimum spanning tree is:");
  printf("\n----------------------------------------------------");

  for(i=0;i< tot_node-1;i++)
  {
   printf("\n Edge {%d,%d} and Weight=%d",tree[i][0],tree[i][1],G[i].length);
  }
  printf("\n----------------------------------------------------");
  printf("\n Total Minimum path Length is= %d",sum);
  printf("\n----------------------------------------------------");
 }
 else
 {
  printf("There Is No Spanning Tree");
 }
}






int Minimum(int n)
{
 int i,small,pos;
 small=INFINITY;
 pos=-1;

 for(i=0;i< n;i++)
 {
  if(G[i].length< small)
  {
   small=G[i].length;
   pos=i;
  }
 }
 return pos;
}
int find(int v2,int parent[])
{
 while(parent[v2]!=v2)
  v2=parent[v2];

return v2;
}
void merge(int i,int j,int parent[])
{
 if(i< j)
  parent[j]=i;
 else
  parent[i]=j;
}


OUTPUT



----------------------------------------------------
KRUSHKAL`s MINIMUM SPANNING TREE ALGORITHM
----------------------------------------------------
 Enter Number of nodes in the Graph:6

 Enter Number of Edges in the Graph:10

--------Enter edges and length----------

Enter edge in form {v1,v2}:1 2

Enter Length from 1 to 2:16

Enter edge in form {v1,v2}:1 5

Enter Length from 1 to 5:19

Enter edge in form {v1,v2}:1 6

Enter Length from 1 to 6:21

Enter edge in form {v1,v2}:2 3

Enter Length from 2 to 3:5

Enter edge in form {v1,v2}:2 4

Enter Length from 2 to 4:6

Enter edge in form {v1,v2}:2 6

Enter Length from 2 to 6:11

Enter edge in form {v1,v2}:3 4

Enter Length from 3 to 4:10


Enter edge in form {v1,v2}:4 5

Enter Length from 4 to 5:18

Enter edge in form {v1,v2}:5 6

Enter Length from 5 to 6:33

Enter edge in form {v1,v2}:4 6

Enter Length from 4 to 6:14

 Enter any key to see Minimum Spanning Tree?
----------------------------------------------------
 The minimum spanning tree is:
----------------------------------------------------
 Edge {2,3}
 Edge {2,4}
 Edge {2,6}
 Edge {1,2}
 Edge {4,5}
----------------------------------------------------
 Total Minimum path Length is= 56
----------------------------------------------------